4 분 소요

본 포스팅은 고려대학교 강필성 교수님의 비정형데이터분석 강의를 보고 정리한 것임을 미리 밝힙니다.

Distributed Representation Models

  • NNLM(2003) - Distributed Representation의 개념을 처음 도입한 Word Embedding계의 시조새
  • Word2Vec(2013) - 주변 단어들의 정보를 활용해서 원하는 단어의 Embedding을 학습 (CBOW vs Skip-gram)
  • Glove(2014) - 단어의 동시발생빈도를 고려해서 Embedding을 학습
  • Fasttext(2017) - 학습 과정에서 보지 못한 단어(OOV)들과 형태소 변화에 대응할 수 있도록 Sub-word 개념을 도입


Word2Vec

이번 포스팅에선 Word2Vec에 대해 이야기한다. Word2Vec은 NNLM의 단점이었던 많은 연산량을 개선하기 위해서 Hidden state를 과감히 제거했다. 하지만 이걸론 부족해 연산량을 더욱 줄이기 위해 계층적 소프트맥스 (Hierarchical softmax)와 네거티브 샘플링 (Negative sampling) 이란 기법을 사용하였다. 이와 관련된 내용은 포스팅에서 차차 설명도록한다.

NNLM vs Word2Vec

  • NNLM : 앞에서부터 시퀀스의 순서를 그대로 유지하며 다음 단어를 예측
  • Word2Vec : 예측하고자 하는 단어의 앞, 뒤의 단어를 활용하여 예측
  • 예시

image-20230407143608031


Word2Vec에는 두 가지 방법이 존재 하는데 바로 CBOW와 Skip-gram이다.

Word2Vec : Skip-gram vs CBOW

  • CBOW : 예측 단어의 주변 단어를 사용하여 중심 단어를 예측하는 방법
    • 예시) The mighty __ Lancelot fought bravely. (__ : knight 예측)
  • Skip-gram : 중심 단어를 사용하여 주변 단어를 예측하는 방법
    • 예시) __ __ knight __ __ __ (__: The, mighty, Lancelot, fought, bravely 예측)

두 가지 방법 중 어느 것이 성능이 더 좋을까? 가볍게 생각해보면 여러 단어를 사용하여 하나의 단어를 맞추는 CBOW이 더 좋을 것 같지만, Skip-gram이 더 좋다고 한다. 이유는 CBOW는 학습 시 Gradient를 한 단어로부터 받지만, Skip-gram은 여러 단어로부터 받기 때문이다. 그러니 Skip-gram을 조금 더 살펴 보도록 하자.


Skip-gram

  • K번째 단어가 주어졌을 때 해당 단어 앞, 뒤로 주어지는 생성 확률을 극대화하는 것이 목표
  • 목적함수는 아래와 같음
\[J(\theta) = \frac{1}{T}\sum_{t=1}^{T}\sum_{-m \leq j \leq m, j\neq0} \log{p(w_{t+j} \| w_t)}\]

$w_t$라는 Center word가 주어졌을 때, +-m(center word로부터 왼쪽, 오른쪽으로 m개)개의 단어가 생성될 확률을 copus의 모든 단어를 고려해서 최대화 하기 때문에 maximize가 된다.

  • 예시 : “나는 친구와 함께 소고기를 먹는다”
    • ‘함께’ 단어를 주어주고 ‘나는’, ‘친구와’, ‘소고기를’, ‘먹는다’ 를 예측하도록 학습
    • 이때 각 단어마다 학습 및 예측을 하는데 (함께, 나는), (함께, 친구와), (힘께, 소고기를), (함께, 먹는다)를 Input으로 넣어 학습한다고 생각
    • 예측할 땐 (함께, 나는), (함께, 친구와) 등 각각 예측한다고 생각


학습과정

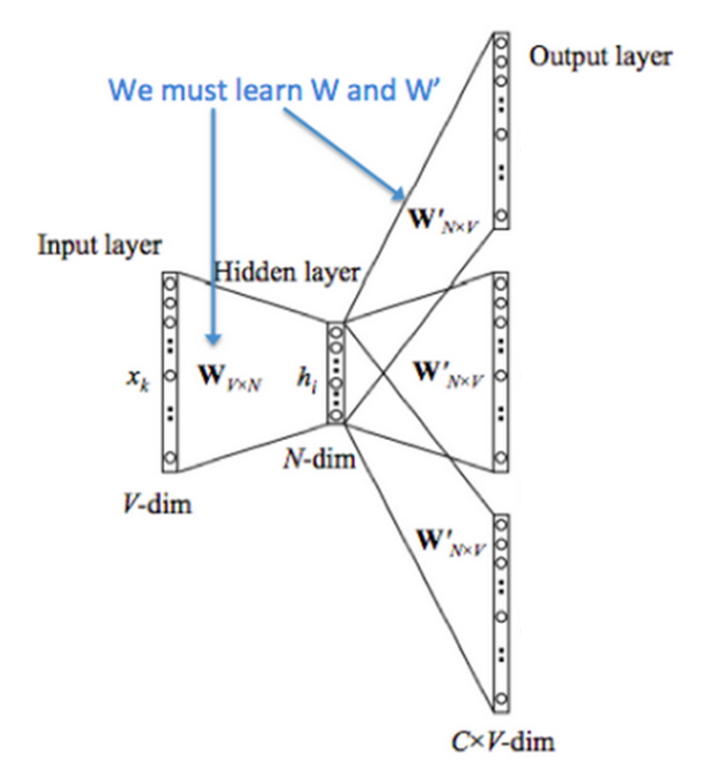
  • 우선 우리는 사전에 정의한 윈도우사이즈에 따른 입력벡터 $x_k$의 원-핫 벡터를 Input layer로 받는다.
    • 예를 들어, “나는 친구와 함께 소고기를 먹는다” 이면, ‘함께’에 대한 벡터는 [0, 0, 1, 0, 0]인 형태로 받는 것이다.
    • 이 때 $x_k$의 사이즈는 $1 \times V$으로 받는다고 치자.
  • Input layer와 Hidden layer 사이를 연결하는 파라미터를 $W_{V \times N}$으로 나타낼 수 있다. 여기서 $x_k$와 $W_{V \times N}$의 내적한 값을 $v_{c}$로 표현한다. 어차피 Input layer가 원-핫 벡터로 이루어져 있기 때문에 $W_{V \times N}$에서도 해당하는 벡터만 가져오게 된다.
  • Hidden layer와 Output layer 사이를 연결하는 파라미터를 $W’_{N \times V}$으로 나타낼 수 있다. 여기서도 내적으로 인해 연산되며, Output layer는 각 단어에 대한 확률값이기 때문에 다시 Vocabulary 사이즈로 만들어주게 된다.
    • 해당 단어에 대한 출력값은 $u_{o}$으로 표현되며 해당 윈도우의 모든 단어의 출력값 $u_{w}$에 대해 소프트벡터에 의해 확률값으로 결과가 출력된다.

center word(c)를 주어졌을 때, 주변 단어(o)를 예측하는 수식 $P(w_{t+j} | w_t)$은 아래와 같이 간단하게 표현할 수 있다.

\[P(o|c) = \frac{exp(v_{o}^{T}v_c)}{\sum_{w=1}^{W} exp({v_{w}^{T}v_c})}\]
  • $P(o|c)$ : center word가 주어졌을 때, 주변(출력) 단어에 대한 예측 확률


수학적 이해

이번엔 목적함수 및 가중치 업데이트에 대해서 알아보자. 우리는 결국 weight matrix인 $W$와 $W’$를 학습시키는 것이 목적이다. Skip-gram 모델에서의 cost function은 ‘중심 단어가 주어졌을 때 주변 단어들이 올 확률’ 이라는 조건부 확률로 풀어나가면 된다. 수식은 아래와 같다.

\[J = -\log P(w_{c-m}, ... , w_{c-1}, w_{c+1}, ... , w_{c+m} | w_{c})\] \[= -\log \prod_{j=0, j \neq m}^{2m} P(w_{c-m+j} | w_{c})\] \[= -\log \prod_{j=0, j \neq m}^{2m} P(u_{c-m+j} | v_{c})\] \[= -\log \prod_{j=0, j \neq m}^{2m} \frac{\exp (u_{c-m+j}^{T} v_{c})}{\sum_{k=1}^{|V|} \exp (u_{k}^{T} v_{c})}\] \[= -\sum_{j=0, j \neq m}^{2m} u_{c-m+j}^{T} v_{c} + 2m \log \sum_{k=1}^{|V|} \exp (u_{k}^{T} v_{c})\]

수식을 한 줄씩 풀어보자.

  1. Cost function을 ‘중심 단어가 주어졌을 때 주변 단어가 올 확률’로 정의했다.
  2. Navie bayse를 이용해 각 단어들은 서로 독립이라는 전제 하에 긴 수식을 Product를 사용해 간결하게 표현할 수 있다. 여기서 $w$는 Vocabulary $V$안에 있는 word이다.
  3. 이는 결국 임베딩된 중심단어가 주어졌을 때, 임베딩된 주변 단어들이 나올 확률을 이렇게 쓸 수 있다. $v_c$는 $W$ matrix의 중심단어에 대한 column을 뜻하며, $u_j$는 $W’$ matrix의 j번째 행을 뜻한다.
  4. 이 조건부 확률은 softmax의 확률로 대치할 수 있다.
  5. 4번의 수식을 풀어서 써주면 다음과 같이 된다.

다음은 Skip-gram의 weight update에 관하여 풀어보자.

학습을 위한 gradient는 다음과 같다. 먼저, $W’$ matrix의 gradient부터 보자. Chain rule을 사용하면

\[\frac{\partial J}{\partial {W'}_{ij}} = \frac{\partial J}{\partial z_{j}} \cdot \frac{\partial z_{j}}{\partial {W'}_{ij}}\]

으로 나타낼 수 있다. 여기서 $z$는 output layer의 score를 뜻한다.

원-핫 벡터로 포현되는 true label(y)로부터 score사이의 gradient는 cross-entropy의 gradient이므로 간단하게 score값과 label의 차이로 구할 수 있다. 그런데, skip-gram 모델에서는 C개의 주변 단어에 대한 cost를 구해야 하기 때문에 loss를 아래와 같이 모두 더해준다.

\[\frac{\partial J}{\partial z_{j}} = \sum_{n=1}^{C}(z_{j} - y_{nj})\]

Output layer의 score부터 projection layer까지의 gradient는 다음과 같이 구할 수 있다.

\[\frac{\partial z_{j}}{\partial {W'}_{ij}} = h_{i}\]

따라서,

\[\frac{\partial J}{\partial {W'}_{ij}} = \sum_{n=1}^{C}(z_{j} - y_{nj}) h_{i}\]

가 된다.

다음으로, $W$ matrix에 대한 gradient를 구해보자. 마찬가지로 Chain rule을 적용하면

\[\frac{\partial J}{\partial W_{ij}} = \frac{\partial J}{\partial z_{j}} \cdot \frac{\partial z_{j}}{\partial h_{i}} \cdot \frac{\partial h_{i}}{\partial W_{ij}}\]

가 된다.

$\frac{\partial z_{i}}{\partial h_{i}} = {W’}_{i}$ 이고,

$\frac{\partial h_{i}}{\partial W_{ij}} = 1$이 되므로

\[\frac{\partial J}{\partial W_{ij}} = \sum_{n=1}^{C}(z_{j} - y_{nj}) W'_{i}\]

가 된다.

최종적으로,

\[{W'}_{ij}^{(new)} = {W'}_{ij}^{(old)} - \alpha \cdot \frac{\partial J}{\partial {W'}_{ij}^{(old)}}\] \[W_{ij}^{(new)} = W_{ij}^{(old)} - \alpha \cdot \frac{\partial J}{\partial W_{ij}^{(old)}}\]

으로 업데이트 할 수 있다.


주의할 점

우리는 학습하고 나면 동일한 크기의 Embbeding matrix인 W와 W’을 얻을 수 있는데, 나중에 단어에 대한 임베딩 벡터를 얻고자 할 때 해당 단어 i번째에 대한 두 matrix의 평균을 계산하거나, 한 쪽의 matrix의 값만 사용해야한다.

하지만 Skip-gram도 차원이 많아 계산량이 증가한다는 문제점을 여전히 갖고 있다. 이에 대응하여 Negative Sampling을 통해 계산량을 줄이고자 하였다. Negative Sampling은 간단하게 마지막 소프트맥스 연산에서 분모 부분이 전체 단어에 대한 확률을 계산하여야 하므로 k개만 따로 뽑아서 그것을 분모로 두자라는 의미이다. 이때 뽑는 것(sampling)에 대해 더 이야기 해보면 자주 등장하는 단어는 누락시킬 확률을 높이고, 덜 등장하는 단어에 대해선 확률을 낮추는 샘플링 기법을 적용한다. 그래서 뽑힌 k개의 단어에 대해서만 소프트맥스 분모로 적용시키자가 취지이다.

CBOW

  • k번째 주변의 단어가 주어졌을 때, 중심 단어가 생성될 확률을 극대화 하는 것이 목표
  • Skip-gram의 반대로 생각해보면 그리 어렵지 않을 것



참고자료

댓글남기기

참고