1 분 소요

차원 축소란

  • 고차원 데이터에서 저차원 데이터로 변환하는 방법 또는 매우 많은 특징으로 구성된 다차원 데이터 세트의 차원을 축소해 새로운 차원의 데이터를 생성 하는 과정
  • 일반적으로 차원이 증가할 경우 데이터 간 거리가 기하급수적으로 증가하기 때문에 희소한 구조를 가지게 되어 모델의 예측에 대한 신뢰도가 떨어지게 됨
  • 일반적으로 차원 축소는 특징(Feature)에 대해 선택(Selection)과 추출(Extraction)으로 나눌 수 있음
    1. 특징 선택(Feature Selection) : 종속성이 강한 불필요한 특징을 제거하는 방법
    2. 특징 추출(Feature Extraction) : 기존 특징에서 더 저차원으로 중요 정보만갖도록 특징으로 압축하는 방법
  • 결론적으로 차원 축소를 통해 데이터를 잘 설명할 수 있는 잠재적 요소를 나타내고자 하는 것 (모델 성능을 위해)


이번 포스팅에는 특징 추출에 대해서만 다루고 있으며, 3가지 차원 축소 알고리즘에 대한 비교만을 언급



차원 축소 알고리즘 (Dimension reduction algorithm)

  • 차원 축소 알고리즘은 아래와 같이 2가지의 종류로 나뉘며 포함하는 알고리즘은 다음과 같음
    • Metrix factorization
      • PCA (prinsipal componant analysis)
    • Neightbor graph
      • T-SNE (t-distributed Stochastic Neighbor Embedding)
      • UMAP (Uniform Manifold Approximation and Projection)


PCA

  • 대표적인 차원 축소 기법이며 Matrix factorization에 근거

  • 분산이 최대인 축을 찾고, 이 축과 직교하며 분산이 최대인 두 번째 축을 찾아 투영시키는 방식 (공분산 행렬의 고유값과 고유벡터를 구하여 산출한다.)

  • 단점 : Linear Hyperplane에 분포된 데이터들을 Projection(투영, 정사영) 하는 것이기 때문에 Non-Linear Hyperplane에 분포된 데이터들에 대해 차원 축소 시 잘 표현될 수 없다는 것이 한계

    ????

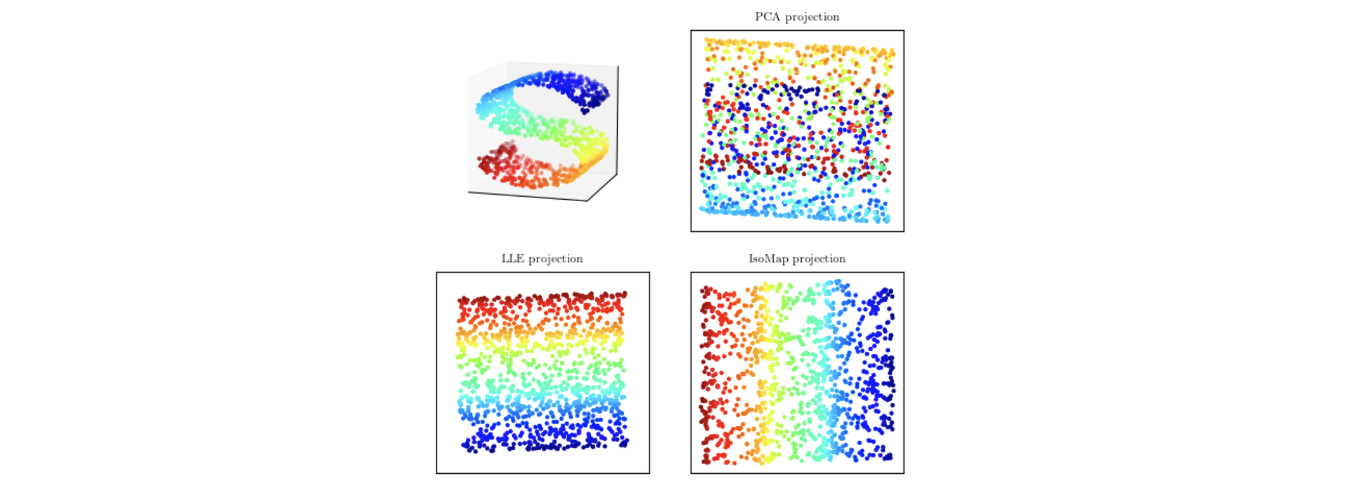
  • PCA에 대한 자세한 설명은 여기서 확인

T-SNE

참고 자료

댓글남기기

참고