[클러스터링] 주요 클러스터링 알고리즘 종류
클러스터링(군집화)이란
- 데이터를 여러개의 부분집합(Clusters)으로 분할하는 것을 의미
- 주어진 데이터들이 얼마나 혹은 어떻게 유사한지 판단할 수 있으며 요약 및 정리에도 매우 효율적인 방법
- 정답(Lable 혹은 y값)을 필요로 하지 않는 비지도학습 알고리즘 중 하나의 방법
- 군집화의 기능적 의미는 숨어있는 새로운 집단을 발견하는 것
- 새로운 군집 내의 데이터 값을 분석하고 이해함으로써 새로운 의미를 부여할 수 있으며 전체 데이터를 다각도로 살펴볼 수 있음
- 예측으로 활용이 가능하며, EDA(탐색적 데이터 분석)에 활용되기도 함
주요 클러스터링 알고리즘
1. K-Means Clustering algorithm (K-평균 군집화 알고리즘)
- Kmeans 알고리즘은 가장 잘 알려진 대표적인 군집화 기법
- 알고리즘이 비교적 간단해 이해하기가 쉽고 직관적
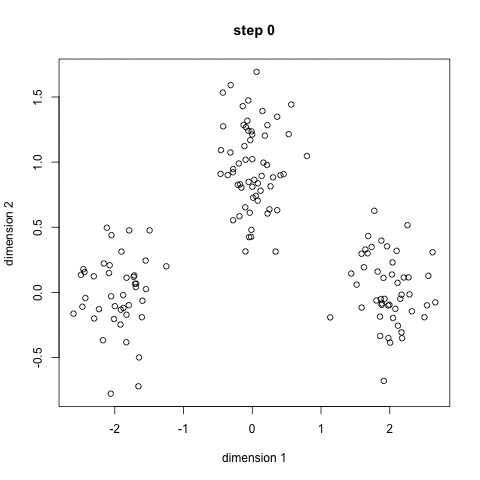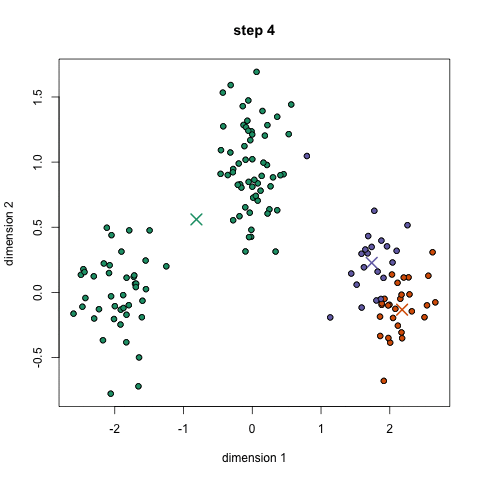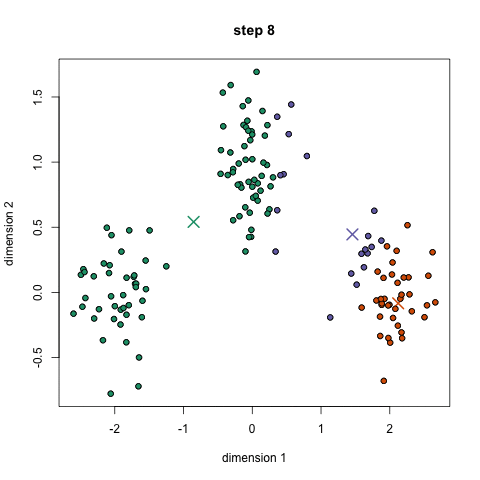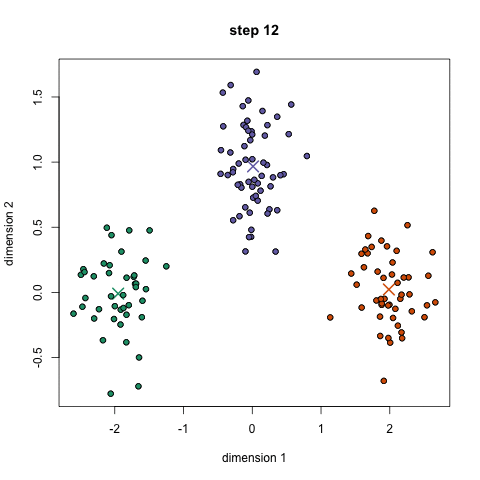
알고리즘의 순서
- 군집의 개수를 선정하고 랜덤하게 초기 중심점을 할당한다. 초기 군집의 개수는 사용자가 지정해야하며 보통 군집의 수가 정해져 있는 경우에 사용하는 것이 좋다.
- 각각의 데이터 포인트들은 각 군집의 중심점(Centroid)과의 거리(다양한 거리척도가 있으며, 보통은 유클리드거리를 사용)를 계산하여 가장 가까운 군집의 중심점이 포함된 군집으로 분류된다.
- 분류된 데이터들에 기반하여 각 군집에 대해 중심점(Centroid)를 다시 계산한다.
- 1~3번의 과정을 각 군집의 중심점(Centroid)의 변화가 없을 때까지 반복한다.
알고리즘의 장단점
- 장점
- 꽤 빠르게 동작함(복잡도 : O(n)) (but 반복횟수가 증가할수록 느려짐)
- 쉽고 간결함
- 단점
- 군집의 개수를 사용자가 지정해주어야 함(사용자 입력변수 존재)
- 랜덤한 초기 중심점에 의해 군집의 결과가 매번 달라질 수 있음
- 거리기반 알고리즘으로 속성의 개수가 많아질수록 군집화 정확도가 떨어짐
2. K-Medians Clustering algorithm (K-중앙값 군집화 알고리즘)
- K-평균 군집화 알고리즘과 달리 군집의 중심점을 평균이 아닌 중앙값을 이용한다는 것이 특징
3. Mean-Shift Clustering algorithm (평균-이동 군집화 알고리즘)
-
데이터 포인트의 밀집 영역을 찾으려고 하는 sliding-window 기반 알고리즘
-
K-평균 군집화 알고리즘과 유사하지만 거리 중심이 아닌 데이터가 모여있는 밀도가 가장 높은 곳으로 군집 중심점을 이동하면서 군집화를 수행함
-
정형데이터보다 컴퓨터 비전 영역의 이미지 혹은 영상 데이터에서 특정 개체를 구분하거나 움직임을 추적하는데 뛰어남
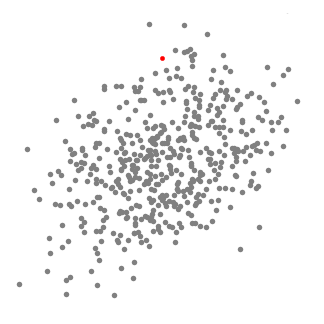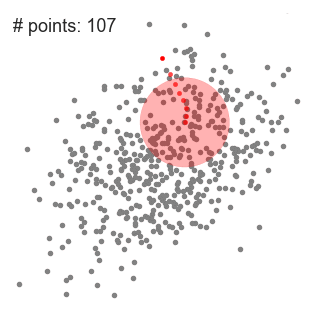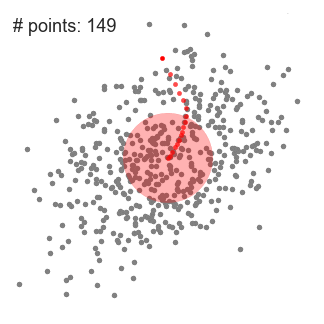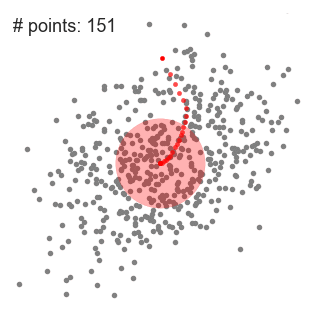
알고리즘 순서
우선 설명을 위해 위의 그림처럼 2차원 공간에서 일련의 점을 고려한다.
- 원 형태의 sliding window(kernel = 반지름(radius), r)를 랜덤하게 선택한 point C에서부터 시작하며, 높은 밀도로 보이는 지역을 각 단계에서 찾기 위해 kernel을 반복적으로 옮긴다.
- 반복할 때마다 sliding window는 더 높은 밀도를 갖는 지역으로 center point를 sliding window 범위 내에 있는 평균값으로 옮겨진다.
- 평균값에 따라 sliding window를 계속해서 옮기고, 이 작업은 kernel 안에 더 많은 points를 수납할 수 있는 방향을 찾지 못할 때까지 계속된다.
- 여러 개의 sliding window안에 모든 point가 수납될 때까지 1~3을 반복한다.

검은색 점은 슬라이딩 윈도우의 중심을 나타내며 각 회색점은 데이터 점임
알고리즘의 장단점
- 장점
- 클래스 혹은 그룹의 수를 정할 필요가 없음
- 해당 알고리즘이 자동적으로 발견
- 쉽고 간결함
- 단점
- Kernel = 반지름 r 사이즈의 결정이 중요하게 다뤄지지 않음
4. Density-Based Spatial Clustering of Applications with Noise (DBSCAN) (잡음이 있는 응용 프로그램의 밀도 기반 공간 클러스터링)
- 밀도 기반 클러스터 알고리즘
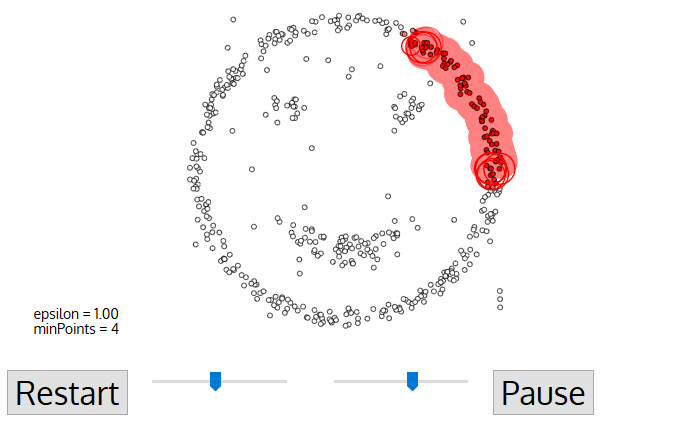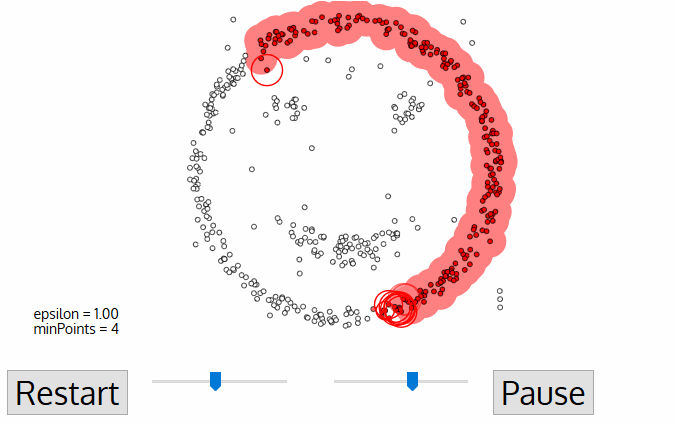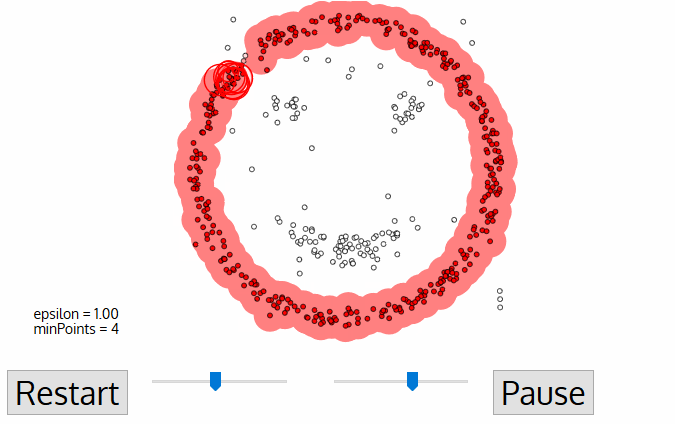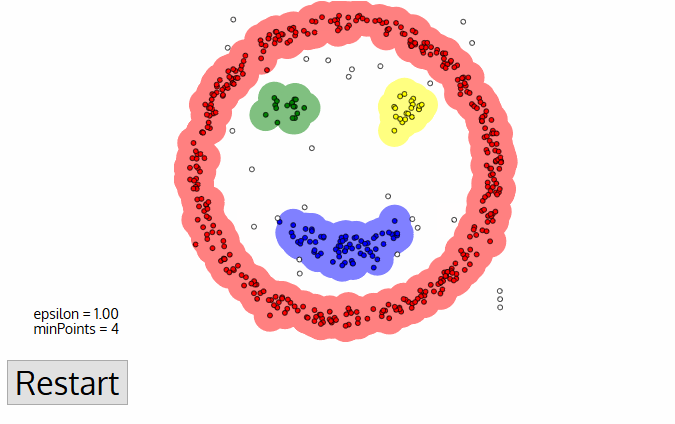
알고리즘 순서
- 방문하지 않은 임의의 데이터 포인트에서부터 시작한다. 거리 $\varepsilon$을 사용하여 거리 내에 있는 이웃 점(neighborhood point)을 추출한다.
- 충분한 숫자의 점들이 이웃으로 위치하고 있다면(munPoints에 따라), 현재 데이터 포인트가 새로운 클러스터의 첫 지점이 되도록 하다. 그렇지 않은 경우, 포인트는 노이즈로 레이블된다(나중에 이 노이즈는 클러스터의 일부가 될 수 있음). 이 모든 두 과정에서 본 점들은 방문된 점으로 분류한다.
- 새로운 군집(클러스터)의 첫 번째 point에서 입실론 거리 내에 있는 이웃 점들도 동일한 군집의 일부가 된다.근방의 모든 점을 동일 군집으로 속하는 이 과정은 그룹에 추가된 새로운 점들에 대해서도 동일한 과정을 거치게 되며 이를 반복한다.
- 2~3의 과정은 모든 점이 결정될 때까지 반복된다.즉 클러스터의 $\varepsilon$근처에 있는 모든 점을 방문하여 레이블을 지정한다.
- 현재 군집화가 끝나면 방문하지 않은 새로운 point가 나오고 다시 위 과정을 반복한다. 모든 점들이 방문될 때까지 과정을 반복하고 마지막 방문으로 처리 될 때 각 포인트는 클러스터 혹은 노이즈로 분류된다.
알고리즘의 장단점
- 장점
- 클래스 혹은 그룹 수를 미리 지정할 필요 없음
- 데이터 포인트가 매우 다른 경우에도 군집으로 만들어내느 K-Menas 알고리즘과 달리 이상치를 노이즈로 식별함
- 임의의 크기와 임의의 모양의 클러스터를 잘 찾음
- 단점
- 클러스터의 밀도가 다양할 때 다른 것만큼 잘 수행되지 않음(밀도가 변할 때 이웃 점을 식별하기 위한 서리 임계값 $\varepsilon$ 및 minPoints의 설정이 클러스터마다 다르기 때문)
- 거리 임계치 $\varepsilon$가 추정하기 어려워지기 때문에 매우 고차원데이터에서도 발생
5. Expectation-Maximization Clustering algorithm utilizing Gaussian Mixture Models (가우스 혼합 모델(GMM)을 사용한 EM(기대값 최대화) 클러스터링)
K-Means 알고리즘과의 비교
- K-Means 알고리즘의 주요 단점 중 하나는 클러스터 센터의 평균 값을 사용하는 것
- 아래 이미지를 참조해보면, 왼편은 육안으로 볼 때 반경이 다른 두 개의 원형 클러스터가 같은 평균에 집중되어 있음. K-Menas 알고리즘은 클러스터의 평균값이 매우 가깝기 때문에 이를 처리할 수 없음.
- 또한 클러스터가 원형이 아닌 경우에도 실패함.
- 결론적으로 K-Menas는 단순히 클러스터 평균을 클러스터 중심으로 사용한 결과인 것.

- GMM은 더 많은 유연성을 제공
- 다만, 데이터 포인트가 가우스 분포(=정규분포)라고 가정 (평균을 잉요해 원이 되어야 한다는 것 보다 덜 제한적인 가정임).
- 클러스터 모양을 나타내는 ‘평균’ 및 ‘표준편차’인 두 개의 파라미터가 존재.
- 2차원으로 예를 들면, 클러스터는 어떠한 종류의 타원형(x, y 축 안에서 표준편차를 갖기 때문에)도 가질 수 있다는 얘기. 이는 각 가우시안 분포는 하나의 클러스터로 할당됨
- 각 클러스터 (예: 평균 및 표준편차)에 대한 가우스의 파라미터를 찾기 위해 Expectation-Maximization(EM)이라는 최적화 알고리즘을 사용
- 아래 그림은 GMM을 사용하여 EM 최적화를 진행하는 프로세스를 보여줌
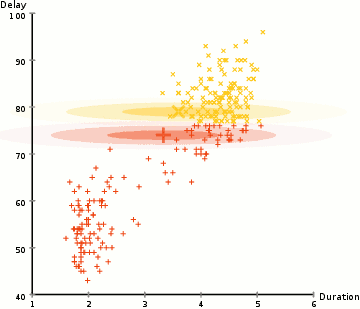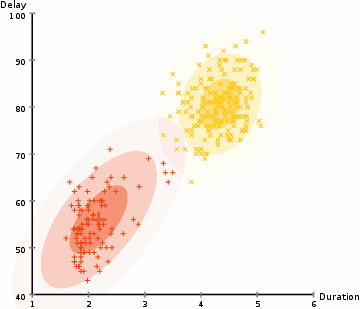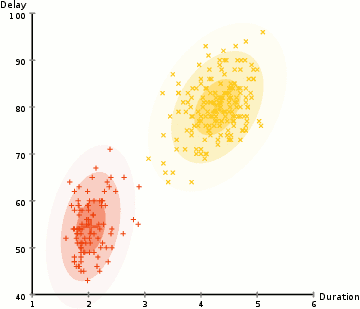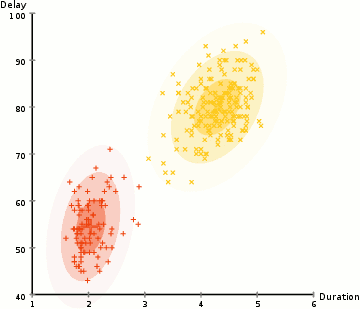
알고리즘 순서
- 클러스터의 수를 정하고, 각 클러스터의 가우스 분포 파라미터를 무작위로 초기화한다. 이후 EM알고리즘을 통해 최적의 파라미터를 찾게 될 것이다.
- 각 클러스터에 대해 가우시안 분포들의 각 데이터 포인트가 특정 클러스에 속할 확률을 계산한다. 가우시안의 중심부에 가까운 point는 해당 클러스터에 속할 가능성이 더 높다. 이는 대부분의 데이터가 클러스터의 중심부에 더 가깝다고 가정한다.
- 이 확률에 기초하여 클러스터 내의 point의 확률을 최대화하기 위해 가우스 분포에 대한 새로운 파라미터 세트를 계산한다. point 위치의 가중치를 적용한 합계를 이용해 이루어지며 가중치는 point가 특정 클러스터에 속할 확률이다. 위의 그림의 노란색 클러스터를 예시로 들면, 첫 번째 반복시 해당 분산은 랜덤하게 정해지지만 대부분의 노란색 points가 오른쪽으로 향해 가는 것을 볼 수 있다.확률로 가중치 합계를 계산할 때 가운데 근처에 몇 가지 point가 있더라도 대부분이 오른쪽에 있다. 따라서 자연적으로 분포의 평균은 그 점 집합에 더 가깝게 이동한다. 따라서 표준편차가 변경되어 확률에 의해 가중된 합을 최대화하기 위해 이러한 점에 더 적합한 타원을 만든다.
- 2~3의 과정은 반복 시마다 많이 달라지지 않는 선에서 집합이 만들어질 때까지 반복된다.
알고리즘의 장단점
- 장점
- 클러스터의 공분산 측면에서 훨씬 유연 (이는 표준편차 파라미터로 인해 클러스터가 원으로 제한되기 보단 타원 모양을 취할 수 있음)
- 확률을 사용하기 때문에 point별로 여러 개의 클러스터를 가질 수 있음
- Mixture Model 중에선 학습속도가 빠른 편
- 단점
- 클러스터의 개수를 의미하는 가우시안 분포의 개수를 사용자가 지정해야 함(하지만 BIC(Bayesian information Criterion) 방식으로 최적화 개수를 찾을 순 있으며, scikit-learn 패키지에서도 해당 기능을 제공)
- 가우시안 분포마다 충분한 데이터 포인트들이 있어야 모수 추정이 잘 이루어짐
댓글남기기